如何使用 Python 可视化声音

那里有大量的音乐和语音数据。还有有趣的应用程序与之配合使用。我们将向您展示如何使用 Python 将声音可视化。

近年来，音频数据分析变得越来越重要。各大科技公司纷纷推出流行的虚拟助手产品，这些产品在世界各地的智能手机和家庭中越来越常见。它们主要是在分析语音数据并从中提取信息的模型的基础上开发的。

音频数据分析的应用范围很广，这是一个值得探索的丰富主题。在本文中，我们将重点介绍音频数据分析过程的一个基本部分——绘制音频文件的波形和频谱。

本文面向具有更多数据分析背景知识的人士。如果您是初学者，正在寻找一些资料来快速掌握数据科学，请查看 此主题 .

打开WAV文件

音频文件有多种格式。您可能熟悉 MP3，它使用有损压缩来存储数据。FLAC 等格式使用无损压缩，允许从压缩数据中完美重建原始数据。我们的音频文件采用 WAV（波形音频文件）格式，未经压缩。因此文件大小可能会很大。

我们将要查看的声音文件是一首以钢琴开始的快节奏歌曲。铃声和拍手声等其他声音贯穿整首歌曲，在曲目的两个点处有吉他弹奏部分。值得一提的是音频录音中的这些特征，因为我们可以在稍后绘制波形和频谱时识别其中的一些特征。

要打开我们的 WAV 文件，我们使用 wave 模块，可以按如下方式导入和调用它：

>>> import wave
>>> wav_obj = wave.open('file.wav', 'rb')

' rb ' 模式返回一个 wave_read 对象。使用 ' wb ' 打开文件会返回一个 wave_write 对象，该对象的方法与前一个对象不同。您还可以使用语句 with 打开文件，如我们 在此处 那样。如果您有兴趣了解有关如何以编程方式处理大量文件的更多信息，请查看 本文 .

声波是连续量，需要以一定的时间间隔进行采样才能将其数字化。采样率量化了每秒采集的声音样本数量。我们可以使用以下方法访问此信息：

>>> sample_freq = wav_obj.getframerate()
>>> sample_freq
44100

采样频率量化了每秒的采样数。在本例中，采样频率为每秒 44,100 次，相当于 CD 音质。单个帧或样本的数量由以下公式给出：

>>> n_samples = wav_obj.getnframes()
>>> n_samples
5384326

我们现在可以计算音频文件的长度（以秒为单位）：

>>> t_audio = n_samples/sample_freq
>>> t_audio
122.09356009070295

音频文件以立体声录制，即在两个独立的音频通道中录制。这给人一种声音来自两个不同方向的感觉。我们可以按如下方式检查通道数：

>>> n_channels = wav_obj.getnchannels()
>>> n_channels
2

下一步是获取信号的值，即该时间点的波的幅度。为此，我们可以使用该 readframes() 方法，该方法接受一个参数 n，定义要读取的帧数：

>>> signal_wave = wav_obj.readframes(n_samples)

上的内置函数 type() 自行检查 signal_wave 。要从中获取信号值，我们必须求助于 numpy：

>>> import numpy as np
>>> signal_array = np.frombuffer(signal_wave, dtype=np.int16)

这将以一维数组的形式返回两个通道的所有数据。如果你检查 的形状 signal_array ，你会发现它有 10,768,652 个元素，正好是 n_samples * n_channels 。要将数据拆分到各个通道，我们可以使用一个巧妙的小数组切片技巧：

>>> l_channel = signal_array[0::2]
>>> r_channel = signal_array[1::2]

现在，我们的左右声道是分开的，都包含 5,384,326 个整数来表示信号的幅度。

接下来，我们展示一些如何绘制信号值的示例。我们在这里将数据存储在数组中，但对于许多数据科学应用程序来说，pandas 非常有用。查看 这篇 关于可视化存储在数组中的数据的 DataFrame .

绘制信号幅度

在绘制信号值之前，我们需要计算每次采样的时间。这只是以秒为单位的轨道总长度除以样本数。我们可以使用 linspace() from 来 numpy 创建一个时间戳数组：

>>> times = np.linspace(0, n_samples/sample_freq, num=n_samples)

对于绘图，我们将使用 pyplot 中的类 matplotlib 。如果您需要一些有关使用 Python 进行绘图的背景资料，我们有一些文章。以下是 的简介 第 1 部分 和 第 2 部分 matplotlib .

为了简单起见，我们只绘制一个通道的信号。让我们设置图形，并绘制如下时间序列：

>>> import matplotlib.pyplot as plt
>>> plt.figure(figsize=(15, 5))
>>> plt.plot(times, l_channel)
>>> plt.title('Left Channel')
>>> plt.ylabel('Signal Value')
>>> plt.xlabel('Time (s)')
>>> plt.xlim(0, t_audio)
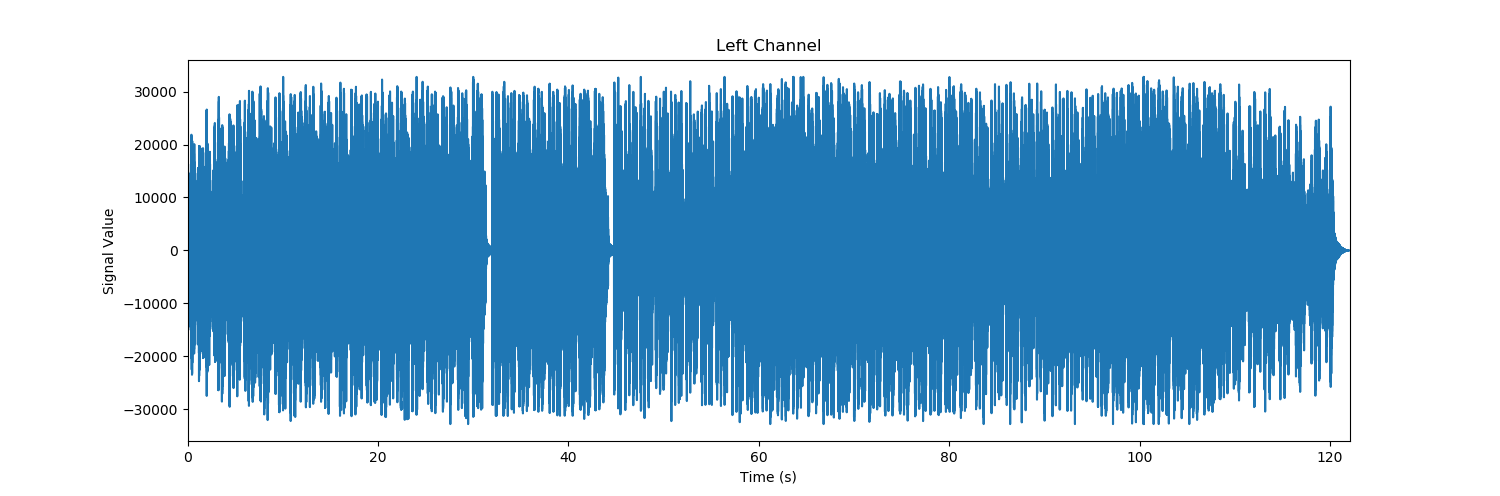
>>> plt.show()

这将在新窗口中打开下图：

我们看到振幅在前 6 秒内逐渐增大，此时铃声和拍手声开始出现。铃声中有两个短暂的停顿，分别位于 31.5 秒和 44.5 秒，这在信号值中很明显。第二次停顿后，主乐器在吉他和钢琴之间交替，这在信号中大致可见，其中吉他部分的振幅较低。然后，在曲目结尾处有一个振幅较低的结尾。

绘制频谱

现在，让我们看一下频谱，也称为声谱图。这是不同频率信号强度的直观表示，向我们展示了哪些频率在时间函数中占主导地位：

>>> plt.figure(figsize=(15, 5))
>>> plt.specgram(l_channel, Fs=sample_freq, vmin=-20, vmax=50)
>>> plt.title('Left Channel')
>>> plt.ylabel('Frequency (Hz)')
>>> plt.xlabel('Time (s)')
>>> plt.xlim(0, t_audio)
>>> plt.colorbar()
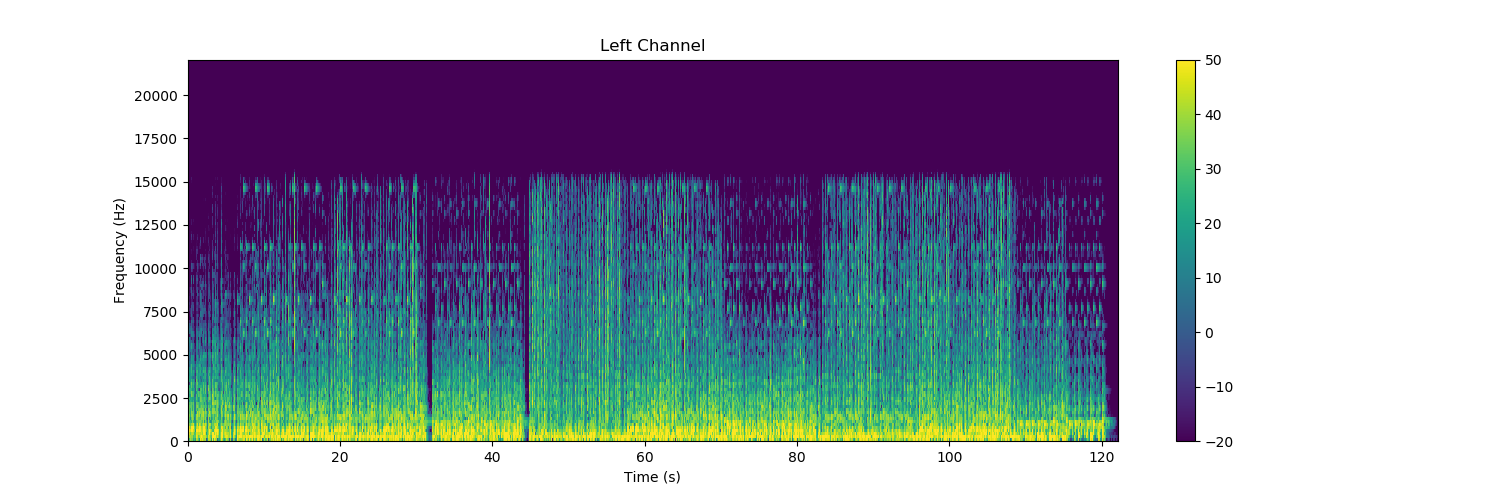
>>> plt.show()

以下图表在新窗口中打开：

在上面的绘图代码中，vmin 和 vmax 被选择来显示主导此录音的较低频率。事实上，整个音轨的主导频率低于 2.5 kHz。您可以看到不同乐器和音效的效果，特别是在约 10 kHz 到 15 kHz 的频率范围内。每种乐器和音效在频谱中都有自己的特征。

从这往哪儿走

使用 Python 绘制波形和频谱为更深入地分析声音数据奠定了基础。也许您可以进一步量化录音每个部分的频率。与钢琴部分相比，吉他部分的平均频率是多少？在这里，我们只查看了一个通道。这里材料的另一个扩展是绘制两个通道并查看它们的比较情况。尝试绘制通道之间的差异，您会看到波形和频谱中出现了一些新的有趣特征。