Python 中的组合迭代器简介

组合迭代器是一种提供构建块的工具，可提高代码效率。本介绍将向您展示 Python 中一些最有用的组合迭代器。

数数

在本文中，我想简单介绍一下 Python 中的组合迭代器。

数学意义上的组合学是关于计数的。它可以帮助我们计算某事物的排列数（一副牌有多少种可能的排列方式）或组合数（不同颜色的球有多少种独特的排列方式）。要做到这一点，我们需要一组对象来采取行动——需要迭代的东西。

在 Python 中，可迭代对象（通常称为 可迭代 ）是数据组。您可能熟悉的一些常见可迭代对象是 列表、元组、集合 和 数组 ，您可以使用 for 循环对其进行迭代。这些可迭代对象通常填充整数值、浮点数或字符串。字符串本身是可迭代对象，因为您可以循环遍历其中的所有字符。一个相关概念是迭代器 ， 它是一个返回可迭代对象的下一个元素的对象。

将这两部分放在一起，我们最终得到了组合迭代器。它们可以帮助您计算事物：例如，列表中数字的不同组合或字符串的不同排列。itertools 模块提供了帮助您完成所有这些操作的功能，该模块随 Python 的默认安装一起提供。

在我们深入了解 Python 中的组合迭代器之前，值得仔细研究一下如何迭代可迭代对象。如果您是 Python 的完全初学者，请查看本 课程 ，该课程旨在满足没有编程经验的人的需求。

迭代器、可迭代对象和迭代

我们说过，可迭代对象是数据组——例如整数列表。但要获取列表中的各个元素，我们需要一个迭代器。如果您对详细信息感兴趣，请查看 Python 文档 。 我们可以定义一个包含一些整数值的列表，如下所示：

x = [1, 2, 3]

需要注意的是，执行此操作时，整个列表都会保存到内存中。要遍历此列表，标准方法是使用循环 for ，但还有另一种方法，即使用一些鲜为人知的 Python 内置函数，特别是 iter() 和 next() 。您可以直接在方法中定义可迭代对象 iter() 并打印元素，如下所示：

>>> x_iterator = iter([1, 2, 3])
>>> print(next(x_iterator))
1
>>> print(next(x_iterator))
2
>>> print(next(x_iterator))
3
>>> print(next(x_iterator))
StopIteration

从 x_iterator 类型为 的 <class 'list_iterator'> 创建了一个 [1, 2, 3] 类型为 的 <class 'list'> 。这个迭代器可以看作是一个接一个的整数流。为了访问整数，我们使用内置 next() 方法对其进行迭代，每次迭代一个值。一旦访问，整数就会从流中移除，迭代计数将存储为内部变量，这允许迭代器在 next() 再次调用该方法时记住其位置。迭代完成后，它会引发异常 StopIteration ，因为所有元素都已被移除。 这意味着迭代器只能遍历一次。

在这个阶段，您可能想知道 for 循环与所有这些有何关系，因为迭代通常是这样进行的。事实上，循环 for 是一种迭代器。在执行 for 循环之前，会在后台创建一个迭代器对象，然后执行迭代，直到 StopIteration 出现异常。对于那些需要复习 for 循环的人，请查看 这篇 文章。因此，使用 for 循环，可以通过以下方式实现迭代：

>>> x_iterator = iter([1, 2, 3])
>>> for element in x_iterator:
...    print(element)

请注意，我们必须重新定义， x_iterator 因为我们已经 StopIteration 在第一个示例中遇到了。这就是 x 直接遍历列表和遍历 x_iterator 。整个列表 x 存储在内存中，可以反复遍历，而是 x_iterator 一个整数流，只能遍历一次。因此，使用 x_iterator 更有效率，这在处理大量数据时确实开始发挥作用。

itertools 迭代器

顾名思义，该 itertools 在此处 找到文档 。此模块中有许多函数，它们都属于以下三个类别之一：无限迭代器（想象一个 while 循环）、终止迭代器（想象一个 for 循环）和组合迭代器（计数事物）。

它们被设计为内存高效，因此此模块中的函数返回迭代器，以数据流的形式提供结果。由于数据仅在需要时生成，因此可迭代对象不需要存储在内存中。这可能有点令人困惑，所以让我们看一些具体的例子，了解如何调用这些函数并检索结果。我们将要介绍的函数属于组合函数，可用于提高代码效率。

产品（）

我们将要介绍的 itertools 第一个 product() ，它实现了两个可迭代对象的笛卡尔积。下图说明了它的工作原理，相当于从两个一维向量创建一个二维数组。输入可以是任何可迭代对象，输出则以元组列表的形式给出。如果您想要一个真正的数组，则必须重新转换输出，例如使用 NumPy。

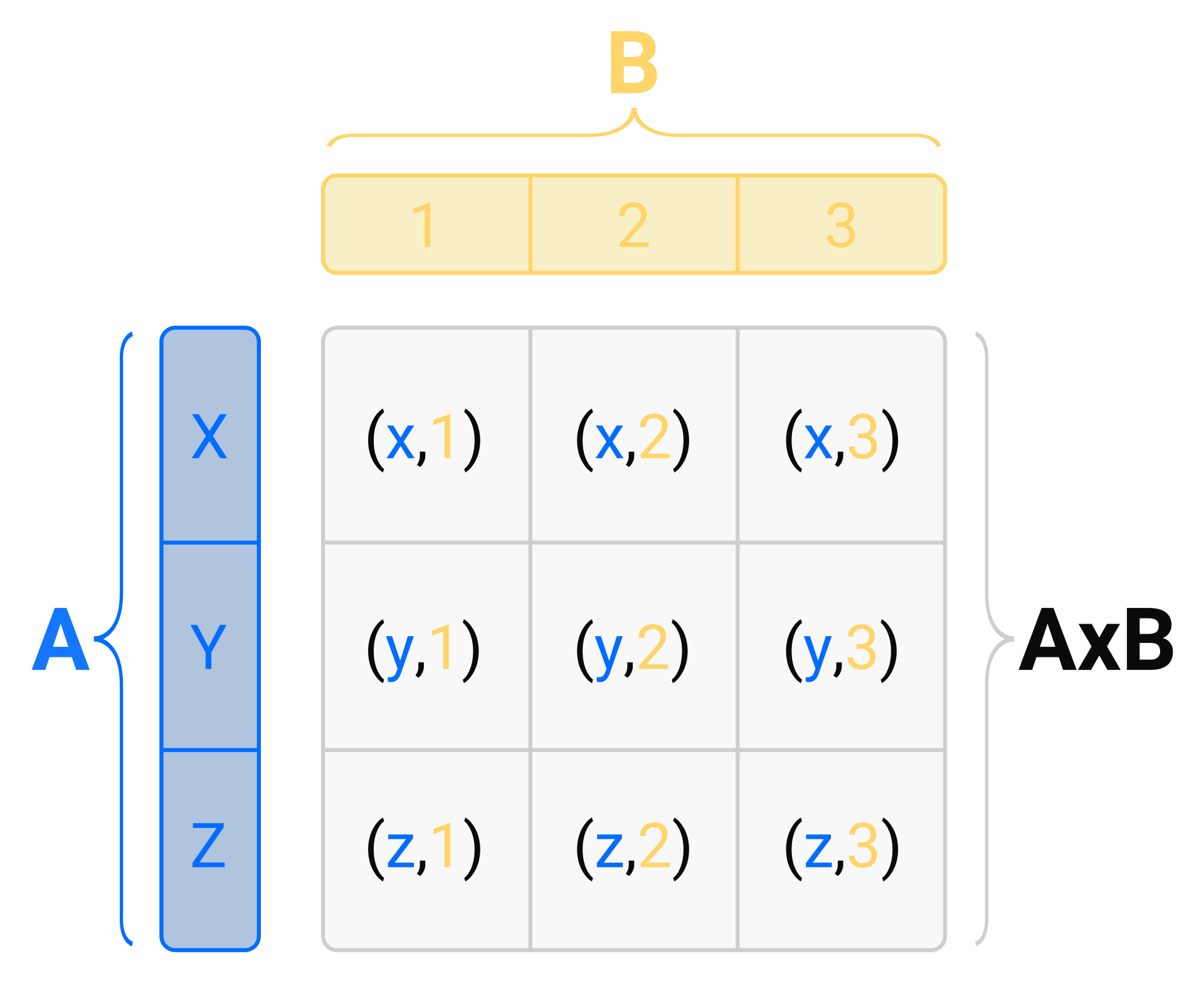
(x, y, z) x (1, 2, 3) 的笛卡尔积

要在 Python 中实现这一点，只需调用下面的函数即可 itertools ：

>>> result = itertools.product(['x', 'y', 'z'], [1, 2, 3])

结果变量现在是一个类型为 的迭代器 <class 'itertools.product'> 。这本质上与 x_iterator 前面示例中的 相同，因此，只能使用 for 循环或 方法迭代一次 next() 。或者，您可以将其重新转换为列表，此时整个结果 存储在内存中，可以多次迭代 .

>>> result_list = list(result)

还要注意，输入是字符串列表和整数列表。生成的元组列表保留这些数据类型。此函数还可用于计算可迭代对象与其自身的笛卡尔积，使用可选的 repeat 参数。以下两行给出相同的结果：

>>> itertools.product(['x', 'y', 'z'], repeat=2)
>>> itertools.product(['x', 'y', 'z'], ['x', 'y', 'z'])

尝试不使用 itertools 库来解决这个问题，看看你能得出什么结论。最明显的解决方案是使用两个 for 循环，并循环遍历两个列表中的每个元素，这需要 3 行代码。相反，使用函数可以更有效地解决这个简单的问题 product() 。

排列()

排列是按特定顺序排列对象。还记得介绍中的一副牌的例子吗？一副 52 张牌中有多少种不同的排列方式？它们是什么样子的？

实际上，用 Python 计算这些排列并不简单。对于 52 张牌，就有 52！（大约 8 x 10 ⁶⁷ ）种排列。这个数字非常大，以至于每当你拿起一副洗好的牌时，你手中可能拿着一种以前从未存在过、以后也不会再存在的排列！所以请不要尝试在家里计算这个数字——如果你这样做，你的电脑不会感谢你的。

考虑一个更容易处理的问题，我们可以用 Python 计算排列。三种不同颜色的球有多少种可能的排列方式，它们看起来是什么样子的？

>>> balls = itertools.permutations(['red', 'green', 'blue'])
>>> for permutation in balls:
...     print(permutation)
...
('red', 'green', 'blue')
('red', 'blue', 'green')
('green', 'red', 'blue')
('green', 'blue', 'red')
('blue', 'red', 'green')
('blue', 'green', 'red')

有 3！= 3 x 2 x 1 = 6 种排列。也可以通过将球重新转换为列表并使用 len() 内置函数获取长度来计算。自己尝试一下。如果您想了解有关 Python 中一些最有用的内置函数的更多信息，请查看本 course .

组合（）

下一个函数提供了在 Python 中计算组合的功能。这与排列略有不同，因为在考虑组合时项目的顺序并不重要。还有一个额外的关键字参数， r 它定义要查找的组合的长度。

让我们再看一下彩色球的例子，并将黄色球添加到列表中：

>>> balls = itertools.combinations(['red', 'green', 'blue', 'yellow'], r=3)

关键字 r=3 表示我们感兴趣的是考虑 3 个球的组合，其中有 4 个，如下所示：

>>> for combination in balls:
...     print(combination)
...
('red', 'green', 'blue')
('red', 'green', 'yellow')
('red', 'blue', 'yellow')
('green', 'blue', 'yellow')

组合与替换（）

顾名思义，下一个函数与 类似 combinations() ，但它允许项目 重复多次 。这会产生更多可能的组合，因此我们只在下面显示一个子集，但请自行查看完整列表：

>>> balls = itertools.combinations_with_replacement(['red', 'green', 'blue', 'yellow'], r=3)
>>> for combination in balls:
...     print(combination)
...
('red', 'red', 'red')
('red', 'red', 'green')
('red', 'red', 'blue')
...
('blue', 'blue', 'yellow')
('blue', 'yellow', 'yellow')
('yellow', 'yellow', 'yellow')

编码挑战

上面用彩色球的例子演示了一些 itertools 函数是如何工作的，但它们有点枯燥。所以，是时候举一个更相关的例子了。

当你申请编程工作时，招聘经理通常会向申请人发送编码挑战以测试他们的技能。对于那些正在寻找技术工作的人来说， 这是 一篇有用的文章。让我们考虑一下你在下一次求职时可能会遇到的一个更有趣的问题，看看如何 itertools 应用。

问题陈述： “使用任意数量的 50 美元、20 美元和 10 美元钞票，有多少种方法可以兑换 100 美元钞票？”

一种简单的方法是手动生成 2 张钞票、3 张钞票、4 张钞票等的组合，并检查它们的总和是否为 100。这很容易出错，看起来像是一堆 for 循环、 while 循环和 if-else 语句。但认识到钞票的最大可能数量是 10 张（10 美元 x 10 = 100 美元），并且短语“任何数字”都意味着替换，您可以生成一个更有效的解决方案，如下所示：

>>> notes = [50, 20, 10]
>>> result = []
>>> for i in range(1, 11):
...     for combination in itertools.combinations_with_replacement(notes, i):
...         if sum(combination) == 100:
...             result.append(combination)
...
>>> print(len(result))
10

正如我们所展示的，使用 itertools 可以帮助计算 Python 中的笛卡尔积、排列和组合。它通过减少对循环和条件语句的依赖，大大简化了您的代码。原本需要多行才能完成的事情，现在只需一行即可完成。这使得代码更简单、更易读、更高效。

这已经是胜利了，但当你开始使用 itertools 函数作为构建块来为更复杂的基于迭代的算法创建组合表达式时，下一个层次就到来了。Python 还有一些内置迭代器，可以与它们结合使用来 itertools 实现下一个级别的编程。

您想要更多 Itertools 吗？

我们只讨论了这个库中的 4 个函数。值得一看的文档 itertools 可以 更好地了解这个库可以做什么。如果您有兴趣了解更多 itertools ，请尝试恰当命名的 more-itertools 模块。这个模块不随 Python 提供 - 因此您必须自己安装它，但它充满了有用的函数，在您的 Python 旅程中，这些函数肯定会让您的生活更轻松。