二叉树是最复杂的数据结构之一。二叉树之所以如此复杂,原因之一是很难用简单的方式将其形象化。
在本教程中,我将向您展示如何创建自己的 BinaryTreeViewer,以便您在运行时查看树。
您可以在此处查看该项目的源代码: https://github.com/giladbarilan/binary-tree-viewer
什么是二叉树?
二叉树是一种非常常用的基于节点的数据结构。树的每个节点由三个元素组成:
- 节点的值,
- 对左孩子的引用(如果没有左孩子,则可以为空),
- 对右孩子的引用(如果没有右孩子,则可以为空)。
例如,假设我们有一个节点,其值为 1,其左侧子节点的值为 3,其右侧子节点的值为 2。下面是我们绘制树的图的方式:
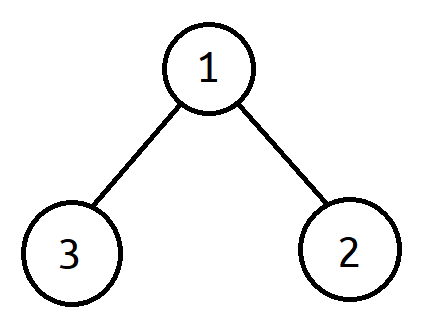
一个节点最多可以有两个子节点,但也可以有一个或没有子节点。当我们想要遍历二叉树中的元素时,我们通常使用递归方法(下面显示了一个示例)。
现在我们知道了二叉树数据结构的工作原理,让我们学习如何在 C# 中实现二叉树结构。
namespace BinaryTreeViewer
{
///
/// Represents a Binary Tree class used for the BinaryTreeViewer.
///
/// The tree node's type.
public partial class BinaryTree
{
private BinaryTree? rightNode; // right node of the binary tree.
private BinaryTree? leftNode; // left node of the binary tree.
public T value { get; set; } // the value of the current node.
public BinaryTree(T value)
{
this.value = value;
this.rightNode = null;
this.leftNode = null;
}
public BinaryTree(T value, BinaryTree? left, BinaryTree? right) : this(value)
{
this.rightNode = right;
this.leftNode = left;
}
public void SetLeftNode(BinaryTree node)
{
this.leftNode = node;
}
public void SetRightNode(BinaryTree node)
{
this.rightNode = node;
}
public BinaryTree? GetRightNode() => this.rightNode;
public BinaryTree? GetLeftNode() => this.leftNode;
public override string? ToString() => this.value?.ToString();
}
} 在上面的代码中,我们用我们讨论过的 3 个元素构建了二叉树结构:值、右孩子和左孩子。问号表示它们是可空的。
让我们做一个简单的例子,演示如何打印二叉树上的所有元素。
//Builds the tree.
BinaryTree tree2 = new BinaryTree(1);
tree2.SetRightNode(new BinaryTree(2));
tree2.GetRightNode().SetLeftNode(new BinaryTree(4));
tree2.SetLeftNode(new BinaryTree(3));
tree2.GetLeftNode().SetRightNode(new BinaryTree(5));
PrintTree(tree2);
//Prints out the tree
public static void PrintTree(BinaryTree tree_)
{
if (tree_.GetLeftNode() != null) //if he has a child from his left.
PrintTree(tree_.GetLeftNode()); //go to his left child family.
if (tree_.GetRightNode() != null) //if he has a child from his right.
PrintTree(tree_.GetRightNode()); //go to his right child family.
Console.WriteLine(tree_.value); //print the current value.
} 基本二叉树算法
在我们开始实施之前,最好先了解一下算法。
让我们回到树的简单例子:
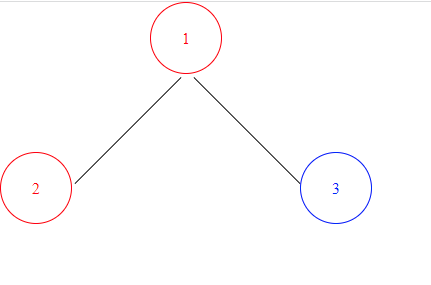
从这个小例子中,我们实际上可以了解如何正确构建树的基础知识。
首先,我们无法预测需要给父节点多少偏移量(以便有足够的空间来绘制树的最左边的节点)。因此,我们需要先找到树的最左边的节点。
一旦我们找到它,我们就会明白我们需要与树的父级有多少偏移。
在这个例子中,我们不能先写父节点,因为我们不知道从左边开始会有多少个节点。如果我们在写节点 1 时在 x 轴上没有任何偏移,那么绘制节点 2 可能会有问题。
二叉树算法的问题
当我们绘制树时,我们与父节点之间的距离是恒定的。在上面的例子中,父节点与节点 3 之间的距离等于父节点与节点 2 之间的距离。因此,该算法可能会遇到菱形图等问题。
什么是钻石图?
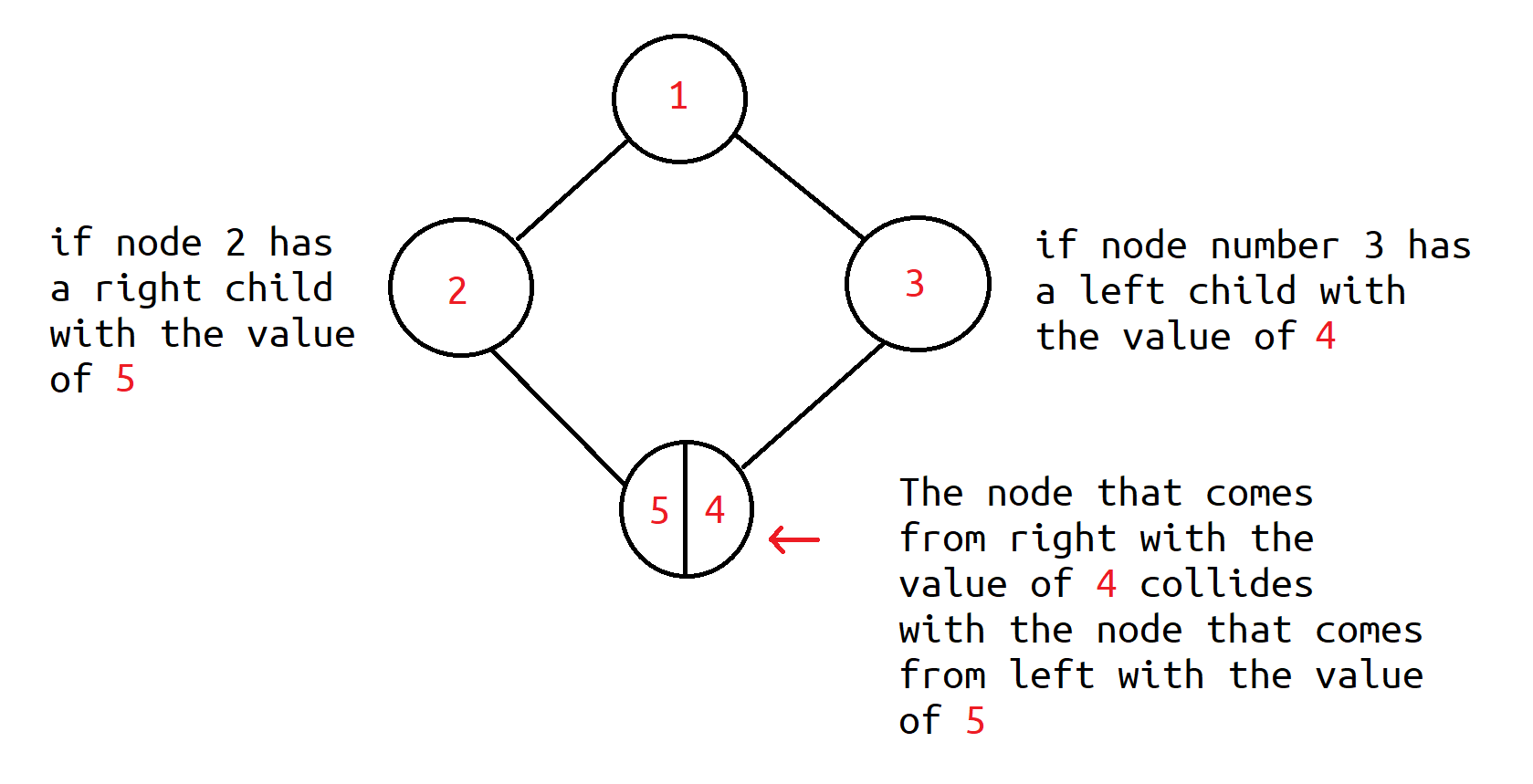
假设父节点有左子节点(节点 2)和右子节点(节点 3)。右子节点(节点 3)有左子节点(节点 4),左子节点(节点 2)有右子节点(节点 5)。
在这种情况下,我们将与子节点(节点 4 和节点 5)发生碰撞,因为它们将被放置在相同的位置。
目前,解决这个问题主要有两种方法:
- 进行预先构建的计算,将树绘制为非对称树,而不必与父级保持恒定的距离。
- 将来自左侧的节点涂成一种颜色,将来自右侧的节点涂成不同的颜色。
第一种实现方式的问题在于,我们使用 BinaryTreeViewer 是为了节省时间。即使使用这种实现方式比使用颜色更整洁、更美观,程序也会太慢,并且会损害我们代码的性能。
因此在本教程中,我们将坚持采用第二种方法来解决菱形图问题(着色)。
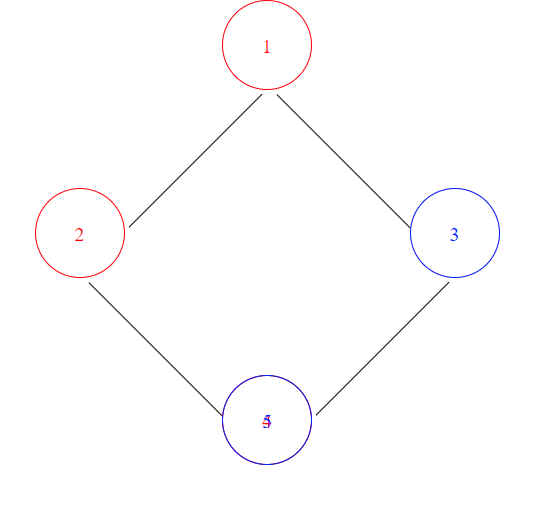
如何实现算法
现在我们已经讨论了二叉树是什么、它们的问题是什么以及我们将使用什么算法来解决这些问题——现在是时候实际实现该算法了。
笔记 : a 部分类 is a class that can be written in separated files, and will be combined on compilation.
让我们从最简单的实现开始,即 BinaryTree 类。
namespace BinaryTreeViewer
{
///
/// Represents a Binary Tree class used for the BinaryTreeViewer.
///
/// The tree node's type.
public partial class BinaryTree
{
private BinaryTree? rightNode; // right node of the binary tree.
private BinaryTree? leftNode; // left node of the binary tree.
public T value { get; set; } // the value of the current node.
public BinaryTree(T value)
{
this.value = value;
this.rightNode = null;
this.leftNode = null;
}
public BinaryTree(T value, BinaryTree? left, BinaryTree? right) : this(value)
{
this.rightNode = right;
this.leftNode = left;
}
public void SetLeftNode(BinaryTree node)
{
this.leftNode = node;
}
public void SetRightNode(BinaryTree node)
{
this.rightNode = node;
}
public BinaryTree? GetRightNode() => this.rightNode;
public BinaryTree? GetLeftNode() => this.leftNode;
public override string? ToString() => this.value?.ToString();
}
} 在部分类的其他部分,我们还有一些方法可用于打印树。
public partial class BinaryTree
{
private BinaryTree? max_left_node;
///
/// Finds the max left offset from the starting node.
///
/// ?, int max_offset) GetMaxLeft()
{
int max_offset = 0;
GetMaxLeft(this, 0, ref max_offset);
return (max_left_node, max_offset);
}
private void GetMaxLeft(BinaryTree head, int left_offset, ref int max_offset)
{
if (head.GetLeftNode() != null)
{
left_offset += 1;
if(left_offset > max_offset)
{
max_left_node = head.GetLeftNode();
}
GetMaxLeft(head.GetLeftNode(), left_offset, ref max_offset);
}
if (head.GetRightNode() != null)
{
left_offset -= 1;
GetMaxLeft(head.GetRightNode(), left_offset, ref max_offset);
}
if(left_offset > max_offset)
{
max_offset = left_offset;
}
}
} 获取最大剩余值
GetMaxLeft 应该为我们提供实现所需的两个细节:
- 哪个节点是树的最左边的节点,以及
- 它与父节点的左偏移量是多少(稍后将乘以一个常数值)。
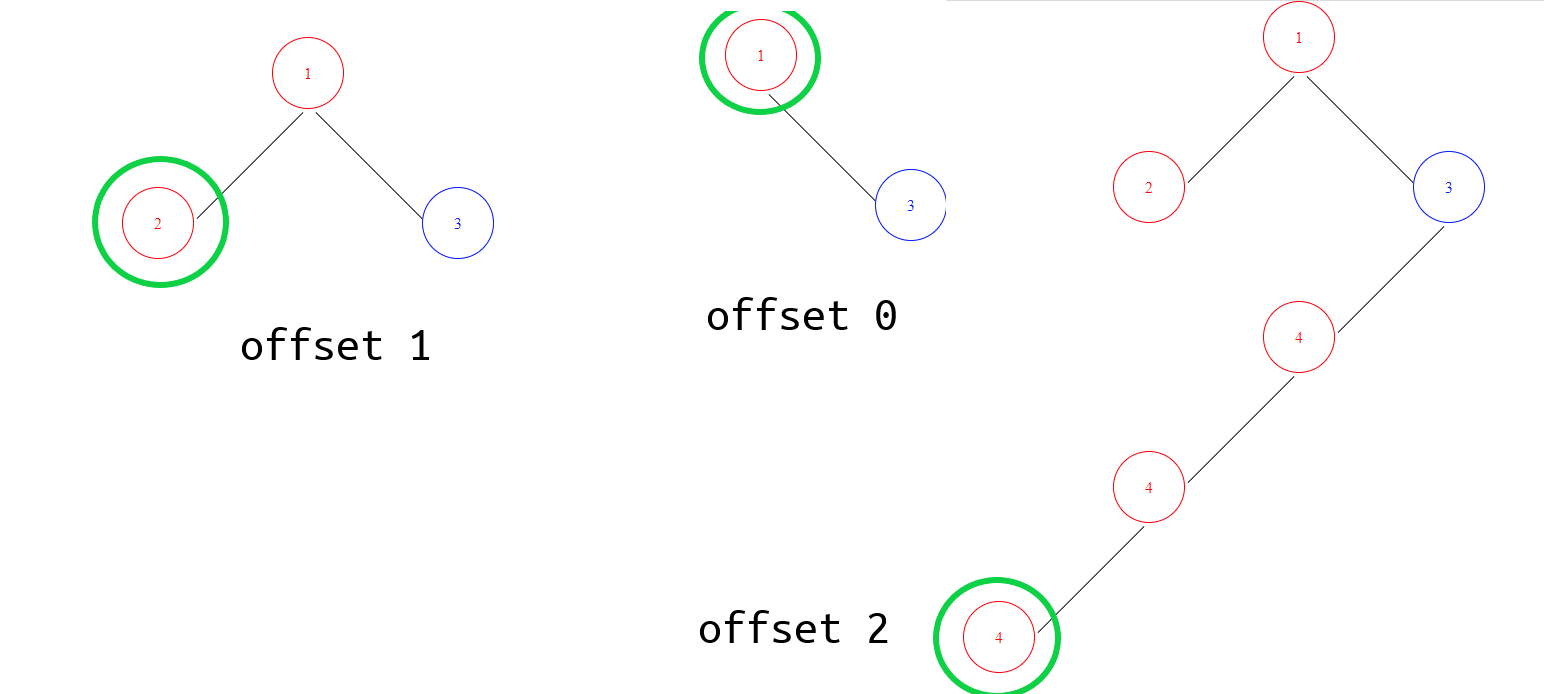
我们将两者作为一个元组返回。
GetMaxLeft 的工作原理
GetMaxLeft 返回树的最左节点相对于父节点的偏移量。它是如何工作的?
每次移动到右侧节点时,我们都会减少左侧偏移值(因为我们正在远离文档的左侧)。每次移动到左侧节点时,我们都会增加偏移值(因为我们正在靠近文档的左侧)。
我们保留从已到达的头部开始的最长偏移量,并通过引用 \' max_offset \' 参数来设置它的值,该参数在非递归 GetMaxLeft 方法中返回。
BTViewer 类
现在我们已经了解了基础知识,是时候面对我们要解决的问题了,那就是如何绘制树。在 BTViewer 类中,我们管理所有树构建过程和临时文件。
using System.Diagnostics;
using System.Text.RegularExpressions;
namespace BinaryTreeViewer
{
///
/// Shows in an HTML document a graph of the tree.
/// RECOMMENDATION: Use break-point on the line of the BinaryTreeViewer.View .
///
public static class BTViewer
{
private static int StartingTempCount = 1; //the starting temp count so we know how many
//trees we've created.
private static int tempCount = 1; // the number of temporary files we've created.
private static readonly string BINTREE_CSS_FILENAME = "BINTREEINITIALIZER.css";
private static string fileName => $"BINTREE{tempCount}.html"; //name structure of BINTREE files.
///
/// Sets the value of tempCount according to the previous saved_trees.
///
static BTViewer()
{
string directory = Directory.GetCurrentDirectory();
if(!Directory.GetFiles(directory).Contains(BINTREE_CSS_FILENAME))
{
File.WriteAllText(BINTREE_CSS_FILENAME, @"#circle{
border-radius: 50%;
display: inline-block;
border: 1px solid black;
}
.a{
padding: 50px;
}
.b{
width: 70px;
height: 70px;
}
.line{
width: 150px;
height: 150px;
border-bottom: 1px solid black;
position: absolute;
}");
}
Regex reg = new Regex(@"BINTREE\d+\.html"); //we check what is the latest binary tree file.
List fileNames = Directory.GetFiles(directory).ToList();
fileNames = reg.Matches(string.Join(" ", fileNames)).Select(x => x.Value).ToList(); //Get the BINTREE files on the directory.
if (fileNames.Count > 0)
{
//we find the next fileName as -> the latest file name count (BINTREE*Number*) + 1
tempCount = fileNames.Select(x => int.Parse(new Regex(@"\d+").Match(x).Value)).Max() + 1; //the next tree to draw.
}
else
tempCount = 1;
StartingTempCount = tempCount;
}
///
/// Writes the full tree into a file by the head.
///
/// (BinaryTree tree)
{
// in case they entered invalid tree.
if (tree == null)
return;
// in case there is only one node on the tree (only the head).
if(tree.GetRightNode() == null && tree.GetLeftNode() == null)
{
InitializeFileStructure(); // we initialize the file structure.
DrawElement(tree, (0, 0), false);
File.AppendAllText(fileName, "